Welcome to the third and last part of the series "Programming loops in M". In the first two parts we dealt with some options to create loop constructs in M with the help of recursive functions or the function List.Generate().
You haven't seen the first two parts of the series yet? Then get to know them here:
In this part of the series I would like to introduce you to a function with which you are able to create the "For-Next"-loop type in M. The function List.Accumulate().
"For-Next"-loops and the functionality of List.Accumulate()
What is a For-Next-loop? A For-Next-loop is a loop statement that repeats or executes a statement contained in it a specified number of times. The number of executions is therefore known or calculable before the start of the loop. In Visual Basic, for example, the basic structure of a "For-Next" loop looks like this:
So [Your Code] is executed five times in the above scheme, because the loop is executed until i reaches the value 5.
Although List.Accumulate() does not understand the keywords "For" or "Next" and cannot include a "counter" i, you can still create a similar behavior using List.Accumulate().
Let's take a closer look at the basic syntax of the function:
Parameter 1
"list"
List.Accumulate() expects a list as the first parameter. The main function of the "list" parameter is to specify the number of loops to be executed. This is done via the number of items contained in the list and not via the items themselves. So in each loop pass List.Accumulate() iterates to the next item in "list".
Parameter 2
"seed"
The parameter "seed" is the start value of the loop or iteration. Since it is of the type "any", this parameter can not only be as number but any type of value, such as tables, lists or records.
Parameter 3
"accumulator"
The last parameter of List.Accumulate() is a function. This function stores the actual expression that is executed in each loop pass. The function "accumulator" has the two parameters "state" and "current". In "state", the intermediate result from the previous loop pass is stored. Meanwhile "Current" always contains the item of the list from parameter "list" reached in the current iteration.
The function List.Accumulate() is also of type "any". Thus appart from all standard value types it can also return any structured value like tables, lists or records as a final result.
Let us visualize this functionality by means of a simple example:
In the following example, an addition is performed using List.Accumulate(), starting from a value of 0 (parameter "seed": brown part). A list containing the numbers from 1 to 10 (green part) is passed to the first parameter "list". In the function definition of the third parameter ("accumulator": purple), "state" and "current" are used to store the result of the loops last pass and the value from "list" for the current iteration.
In the first loop pass, the first item in the list {1..10} (1st item = 1) is referenced. Since the start value is 0, 0 is passed to the "state" parameter. In "current" the current item of the
list is stored, i.e. the value 1 for the first iteration. Within the function "state" and "current" are added and an intermediate result of 1 is determined (0 + 1 = 1).
In the second pass, the second item of the list is referenced, i.e. the value 2. This is passed to the parameter "current", while "state" contains the intermediate result of the last pass, i.e.
1. Accordingly, the result of the second pass is 3 (1 + 2 = 3).
Since the list "{1..10}" contains ten items, this process is repeated ten times. The final result is 55.
What about flexibility when using List.Accumulate()?
List.Accumulate() is an extremely flexible function. In the list in the first parameter you can store items of any type. In most cases these are numbers, but they can also be texts, dates, tables, lists or records. As the following example shows, they can also be mixed lists:
The list in the example (green part) contains a text "A", a record and a list with the numbers from 1 to 8. The choice of such list items is of course strongly bound to what you want to do with these items in the third parameter "accumulator".
Starting from "seed"=0, 1 is added for each loop pass in this example. You can see from result of 3 that the loop was passed three times because the list contains three items. The type of that individual items has no influence on the number of iterations.
The example above shows that you don't have to use the parameters "state" and "current" in the expression of the function in "accumulator". The definition does not use "current", the current item of "list" in the current iteration. If you would not use "state", however, the operation in "accumulator" would not be able to respect the intermediate result of the previous loop pass in the calculation.
In addition to the values in "state" and "current", you can also access values that exist outside of List.Accumulate(), e.g. values from parameters of external functions or variables:
This is possible because the statements on "Environment Concept" and "Closures" I made in the first two parts of this series about recursive functions and List.Generate() also apply to List.Accumulate(). In the "accumulator" (purple part) of "Loop" the parameter "weekday" from the outer function (green part) can also be accessed. This makes it possible to examine the list from the outer variable "ListofDates" (brown part), which contains all dates from January 1st 2010 to June 17th 2018, on how often a certain "weekday" occurs in this period using List.Accumulate(). The "Saturday" e.g. 442 times.
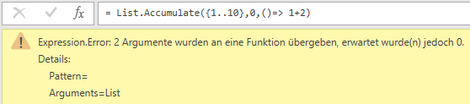
However, this does not mean that you can omit the two parameters in the function definition of "accumulator". Because List.Accumulate() wants to pass the values for "state" and "current" to "accumulator", the absence of these parameters in the function definition, as shown in the picture to the left, is acknowledged with an error message.
Additional flexibility comes in when we are talking about naming the parameters. Instead of "state" and "current" you can alternatively choose names according to your ideas.
In terms of performance, the same statements apply as in the second part of the series on List.Generate(). List.Accumulate() also supports "tail call elimination". The example above illustrates that processes with tens of millions of loops are possible.
What else can you use List.Accumulate() for?
An obvious example for the use of List.Accumulate() is the calculation of running totals or cumulated values.
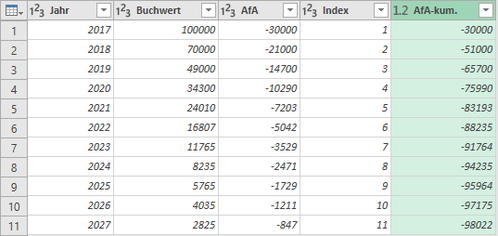
A classic application from the financial area is the calculation of depreciation, that is, the loss in value of assets. The adjacent table "AFA_INDEX" shows an example of a depreciation forecast
for an asset for the years 2017 to 2027 (column "Jahr"), with the corresponding depreciation amounts for the years (column "AfA") and the resulting net book values (column "Buchwert").
In the user-defined column "AfA-kum.", the accumulated depreciation amount for the respective years must be calculated. You can create this calculation with the following function definition:

As list parameter (green part) we inject a list to List.Accumulate(), which is generated by the function List.Range(). List.Range() returns a section of a list, here the column "AfA" from table "AFA_INDEX" ("AFA_INDEX[AfA]"). The second parameter "0" of List.Range() specifies that the list section should start from the lists first entry in the "[AfA]" column, while the third parameter uses the "[Index]" column to specify the length of the list in terms of number of rows. This results in a list with the items -30,000, -21,000 and -14,700 for the third row of the table, because the section returned by List.Range() for this line goes up to [Index]=3.
Such a list with changing length is created for each row of the table and then iterated by List.Accumulate(). Starting from the start value "seed" = 0 (brown color), the values in the list (for line three of the table -30,000, -21,000 and -14,700) are added up using the parameters "state" and "current" in the "accumulator to calculate the accumulated depreciation.
In addition to this frequently shown example for the use of List.Accumulate(), there are a number of other applications in the web. Maxim Zelensky, for example, shows a way to recreate the SUMPRODUCT() function from Excel in Power Query using List.Accumulate(). (Please find his post here)
As indicated above, the use of List.Accumulate() does not necessarily have to be limited to processing numbers. Basically, all types of values can be processed. However, you should always check whether M offers another solution for your problem. As already discussed in the previous parts of this series, solutions with the help of iterations in M should be among the last alternatives you consider.
What did we learn in this series?
With List.Accumulate() we got to know a possibility to create "For-Next"-loops in M. This is done by three parameters. The parameter "list", which determines the number of loop passes that are performed by the number of items the list contains. The parameter "seed", which determines the start value of the loop, and the parameter "accumulator", in which a function is used to define the operation to be performed in each loop pass. Flexible processing with List.Accumulate() is possible, because tables, lists or records can be processed as well as numbers or texts.
Already in the previous parts of the series we got to know two possible solutions for programming of loop constructs in M, recursive functions and List.Generate().
Do you already know the other parts of the series?
We have dealt with the pros and cons, the strengths and weaknesses of these solutions and concepts like "Environments" or "Closures", two concepts that give loops in M even more flexibility.
I hope you enjoyed the series and you will be there for my next contributions. I would be happy if you would share the series with others! Many thanks for reading!
Greetings from Hamburg, Germany
Uwe






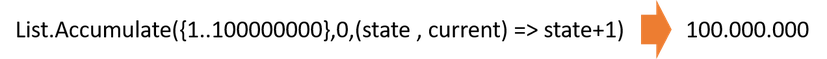



Kommentar schreiben
Jeff Weir (Montag, 22 Juli 2019 06:36)
This is an outstanding series. I have a question: Do you think List.Accumulate can handle the states of multiple input and output tables? Or a clever construction of it?
I’m trying to reconcile data from two different entities regarding movement of shipping containers, by doing a bulletproof fuzzy match on dates. My hard-coded approach involves doing an inner join on the two data sources, removing matches (but keeping a record of them), and then doing subsequent inner joins on the remaining unmatched records. This requires 3 + 3X queries, where X is the amount of days I want to ultimately widen my matching to encompass.
Doing this recursively would radically reduce my code base. I'll post a link to a related forum question in a moment that outlines the challenge...I'd love to hear your thoughts as to whether you believe this is possible.
Jeff Weir (Montag, 22 Juli 2019 06:38)
Link to related forum question, if you're interested:
https://community.powerbi.com/t5/Power-Query/Multilple-recursive-Inner-and-Anti-Joins-for-robust-fuzzy-date/m-p/745368#M24788
Uwe (Dienstag, 23 Juli 2019 21:25)
Hey Jeff,
thanks for reading my post and mentioning it on the Power BI Community site. I'am glad you liked it.
Also thanks a lot for the link. Seems to be quite a nice problem you are facing. Sounds complex. I must admit that I am not quite sure I fully understand what you need to do, so maybe we will need some loops to get the solution:
As stated in the series most of the time I try to avoid recursions in M. So here is a crazy idea without recursion. It might be the case that I did not fully understand what you want to do, but lets give it a try:
How and when is the X (the number of offset days) determined in your example? Could it be determined by joining on ID and Destination and calculating the largest difference in days between the related dates?
Instead of doing recursion to offset all the dates (+-1,2,3...x days) and then join again in each iteration you could create some dummy data in the table in which you are "offsetting" the date.
You could create a column that holds a record with all the dates within the offset range.
E.g. ID=A, Date=19/07/2019 and X = +-3 leads to a list for that line spanning from 16/07/2019 to 22/07/2019.
Expanding that column containing the lists with all the dates for each row will create seven lines (one original and 6 for each dummy date).
After that you could join that table with the other table to find the matches/mismatches you want and do all further processing. All the original data can be identified because they are the ones with identical dates in both the new and the original date column (for a given ID).
I hope I got your point and this new approach can help you on your way.
Ram (Mittwoch, 24 Februar 2021 11:10)
Thank you for sharing these articles. Well organized and detailed!!